2622. Reliable
Nets
You’re in charge of designing a
campus network between buildings and are very worried about its reliability and
its cost. So, you’ve decided to build some redundancy into your network while
keeping it as inexpensive as possible. Specifically, you want to build the
cheapest network so that if any one line is broken, all buildings can still
communicate. We’ll call this a minimal reliable net.
Input. There
will be multiple test cases for this problem. Each test case will start with a
pair of integers n (n ≤ 15) and m (m ≤ 20) on a
line indicating the number of buildings (numbered 1 through n) and the number of potential
inter-building connections, respectively. The following m lines are of the form b1
b2 c (all positive integers) indicating that it costs c to connect building b1 and b2. All connections are bidirectional.
The last test case contains n = m
= 0 and is not processed.
Output. For
each test case you should print one line giving the cost of a minimal reliable
net. If there is a minimal reliable net, the output line should be of the form:
The minimal
cost for test case p is c.
where p is the number of the test case (starting at 1) and c is the cost. If there is no reliable
net possible, output a line of the form:
There is no
reliable net possible for test case p.
Sample input
4 5
1 2 1
1 3 2
2 4 2
3 4 1
2 3 1
2 1
1 2 5
0 0
Sample output
The minimal cost for test case 1 is 6.
There is no reliable net possible for test case
2.
SOLUTION
graphs – biconnected components
Algorithm analysis
A network is reliable if the graph that represents it is
doubly edge connected. Biconnectivity is checked by depth first search – to ensure it, the absence of bridges in the graph is necessary.
If the input graph is not biconnected,
then the required network does not exist. In the case of biconnectivity, graph allows the presence of articulation points.
Using dynamic programming and masks, iterate over all the
edges and try to remove them from the
input graph. That is, iterate over all possible subgraphs. As soon as the next
subgraph is no longer biconnected (it
contains a bridge), stop the search. Among all biconnected subgraphs, look for the one that has the lowest cost.
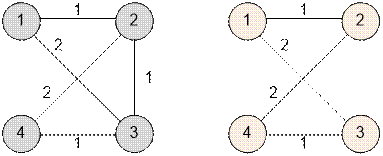
Example
Consider the first graph from the sample. The minimum reliable network is shown on the right. The graph on the right does
not contain bridges, its cost is 6.
Algorithm realization
The input graph is stored in the adjacency matrix g. The arrays used, d and up are used to check if the graph is biconnected. The
cell best[mask] stores the minimum network cost that can be formed from the edges
specified by the mask mask.
#define INF 0x3F3F3F3F
#define MaxV 30
int
g[MaxV][MaxV];
int
used[MaxV], d[MaxV], up[MaxV];
int
best[1<<20];
Store the list of edges of the input
graph in the array of structures E.
struct Edge
{
int u, v,
dist;
}
E[21];
Function dfs that runs depth first search, checks for
bridges in the graph. If a bridge is present, the variable IsBridge is set to 1.
void
dfs (int v, int
p = -1)
{
if (IsBridge)
return;
used[v] = 1;
d[v] = up[v] = time++;
for (int to = 1; to <= n; to++)
{
if ((to ==
p) || !g[v][to]) continue;
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
dfs (to, v);
up[v] = min (up[v], up[to]);
if
(up[to] > d[v]) IsBridge = 1;
}
}
}
Function IsBiconnected returns 1, if
graph is biconnected. For
this, there must be no bridges in the graph.
int
IsBiconnected(void)
{
time = 1; IsBridge = 0;
memset(used,0,sizeof(used));
memset(d,0,sizeof(d));
memset(up,0,sizeof(used));
for(int i = 1; i <= n; i++)
{
if (!used[i]) dfs(i);
if
(IsBridge) break;
}
return
!IsBridge;
}
Compute the minimum network cost that can be formed from the
edges specified by the mask mask. The
length of all edges of subgraph specified by mask equals to CurLen.
int
go(int mask, int
CurLen)
{
int i, opt;
If the
value of best[mask] is already calculated (it is not equal
to INF), then we return it. If the current subgraph is not biconnected,
then stop the search process, the value of best[mask] is set to INF – 1, which is
considered already calculated.
if(best[mask] != INF) return best[mask];
if (!IsBiconnected()) return best[mask] = INF - 1;
best[mask] = CurLen;
Iterate over the edges included in the
subgraph. Remove only one i-th edge from the graph and recursively solve the problem for the
subgraph specified by the mask mask
XOR 2i. The length of the
edges of this graph will be equal to CurLen – E[i].dist.
for(i = 0; i
< m; i++)
{
if (mask
& (1 << i))
{
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
0;
opt = go(mask ^ (1 << i),CurLen -
E[i].dist);
if (opt
< best[mask]) best[mask] = opt;
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
1;
}
}
return
best[mask];
}
The main part of the program. Read the edges of the graph and store them in the array E.
Build the adjacency matrix g. The
edge lengths are stored only in array E. Compute the lengths of all edges in the variable TotLen.
while(scanf("%d %d",&n,&m), n + m)
{
memset(best,0x3F,sizeof(best));
memset(g,0,sizeof(g));
res = INF;
TotLen = 0;
for(i = 0;
i < m; i++)
{
scanf("%d
%d %d",&E[i].u ,&E[i].v,&E[i].dist);
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
E[i].dist;
TotLen += E[i].dist;
}
Find the answer and print it
depending on whether the required reliable network exists. For the graph containing all edges corresponds a mask 2m – 1, consisting of m units.
res = go((1
<< m) - 1, TotLen);
if (res >= INF - 1)
printf("There is no reliable net possible for test case
%d.\n",cs++);
else printf("The
minimal cost for test case %d is %d.\n",cs++,res);
}